
La trave appoggiata caricata con carico distribuitouniforme, risolta con l’applicazione delle equazioni cardinali della statica, è l’argomento di questo esercizio.
La trave, di luce L, appoggiata, è vincolata con una cerniera a sinistra ed un carrello a destra. Il carico è distribuito uniforme.
La risoluzione della trave appoggiata con carico distribuitouniforme è perseguita attraverso l’applicazione delle equazioni indefinite di equilibrio con l’integrazione della funzione carico p(x) e tenendo conto dell’assenza di discontinuità indotte da momenti concentrati M o carichi concentrati P.
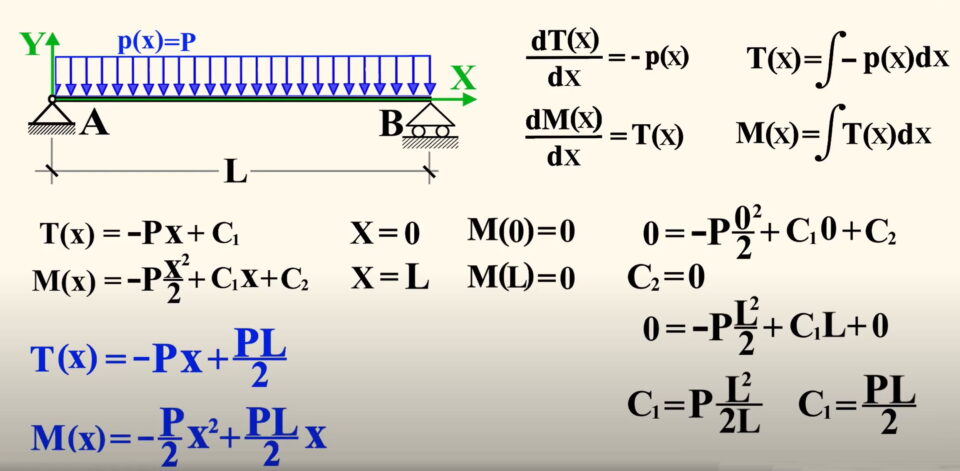
Particolare importanza riveste la scelta delle costanti di integrazione C1 e C2 che si calcolano imponendo il valore nullo del momento flettente all’ascissa X=0 in corrispondenza della cerniera e all’ascizza X=L in corrispondenza del carrello.
Si arriva alla funzione Taglio T(x) e al suo diagramma e poi alla funzione Momento Flettente M(x) e al suo diagramma. Vengono studiate anche le reazioni vincolari.
Il diagramma del Momento Flettente è realizzato con il metodo dell’inviluppo di tangenti e nella lezione si studiano anche le tangenti di estremità al diagramma.
Le lezioni sulle equazioni indefinite di equilibrio si trovano qui.
Un buon ripasso degli integrali lo troverete invece sul canale di Elia Bombardelli a questo link.
Potete inoltre ripassare le reazioni vincolari a questo link.
A seguire trovere la videolezione. Arrivederci alla prossima lezione. Buon studio.
