Ciao, benvenuto/a o bentornato/a su StaticaFacile, questa lezione è dedicata alla SCOMPOSIZIONE DI UNA FORZA compresi alcuni esempi pratici.
Entrando in dettaglio la procedura di scomposizione viene applicata ad alcuni tipi di carichi verticali su travi inclinate.
Questa lezione può interessare agli studenti di Ingegneria o di Architettura, oppure agli studenti degli indirizzi CAT (Costruzioni Ambiente e Territorio) delle scuole superiori.
La lezione esordisce con la definizione di scomposizione di una forza:
Assegnata una forza F e due direzioni arbitrarie a e b rappresentate dalle corrispondenti rette passanti per il punto di applicazione della forza,
scomporre la forza significa trovare due forze la cui risultante sia la forza assegnata F.
La scomposizione di una forza può essere condotta con procedimento grafico e anche con procedimento analitico.
Il procedimento grafico si basa sull’applicazione della regola del parallelogrammo che abbiamo già studiato nella lezione relativa alla somma di due vettori.
Il procedimento analitico si basa invece sull’applicazione del Teorema dei Seni applicato ai triangoli qualsiasi.
Ora, qui di seguito vi anticipo la videolezione.
Dopo di quella troverete qualche dettaglio in più sull’argomento trattato.
Alcuni dettagli sul Teorema dei Seni
Il Teorema dei Seni, considerato un triangolo e assegnato un lato e i due angoli adiacenti, permette di calcolare gli altri due lati incogniti del triangolo.
Il Teorema dei Seni si esprime così:
a/sen(alfa)=b/sen(beta)=c/sen(gamma)
I rapporti tra i lati di un triangolo e i seni dei corrispondenti angoli opposti sono uguali.
Gli asempi associati alla Scomposizione di una Forza
Una volta esposta la parte teorica si passa allo sviluppo di due esempi concreti.

Il primo esempio riguarda la trave inclinata di una copertura in legno sottoposta ai carichi verticali di pertinenza.
Si considera una forza F verticale e si scompone lungo le due caratteristiche direzioni di una trave inclinata:
la direzione parallela all’asse (x) ovvero tangente alla trave e la direzione normale all’asse (y) e quindi ortogonale alla trave.
Questo primo esempio, come anche il secondo che segue, è numerico.
In questo primo caso le forze derivanti dalla scomposizione, oltre che ricavate graficamente, vengono calcolate per via analitica.

Le relazioni utilizzate sono quelle delle componenti di vettore Fx=Fcos(alfa) Fy=Fsen(alfa) dove alfa è l’angolo formato dalla trave inclinata con l’orizzontale.
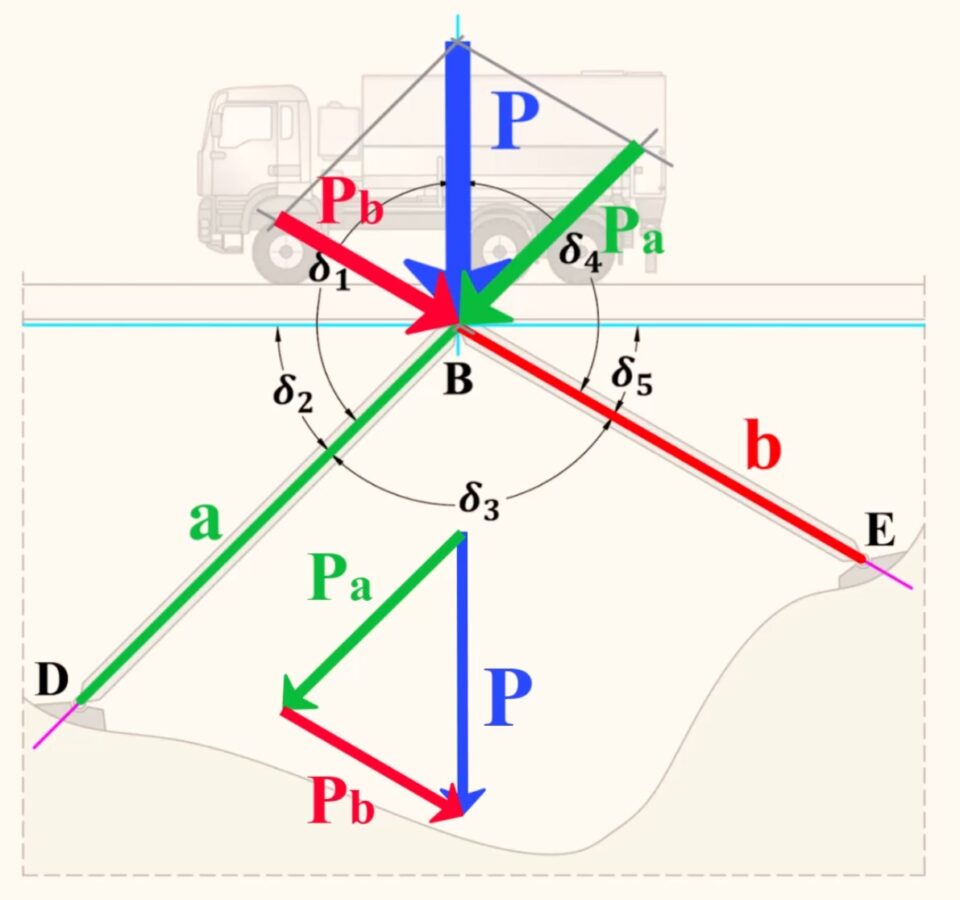
Il secondo esempio riguarda la ripartizione del carico verticale di un ponte su due elementi strutturali diversamente inclinati.
Ma adesso è meglio che tu segua la videolezione, vedrai che ti sarà utile.
Buon studio.
