
In questa lezione espongo il teorema del coseno o di Carnot.
Partiamo dall’enunciato del teorema del coseno o di Carnot per poi passare alla dimostrazione (Figura 1) e infine ad un esempio numerico.
Ricordo velocemente che Lazare Nicolas Marguérite Carnot (1753-1823) fu un uomo di spicco durante la rivoluzione francese e anche nel corso del successivo impero napoleonico
Carnot fu dapprima oppositore di Napoleone ma successivamente divenne un generale dell’armata napoleonica.
Questa è la videolezione sul teorema del coseno o di Carnot:
Ma torniamo all’enunciato del teorema del coseno che recita così:
Il quadrato del lato di un triangolo qualunque è pari alla somma dei quadrati degli altri due lati meno il doppio prodotto dei due lati per il coseno dell’angolo compreso tra i due lati stessi.
Descrizione del procedimento di dimostrazione Teorema del Coseno o di Carnot
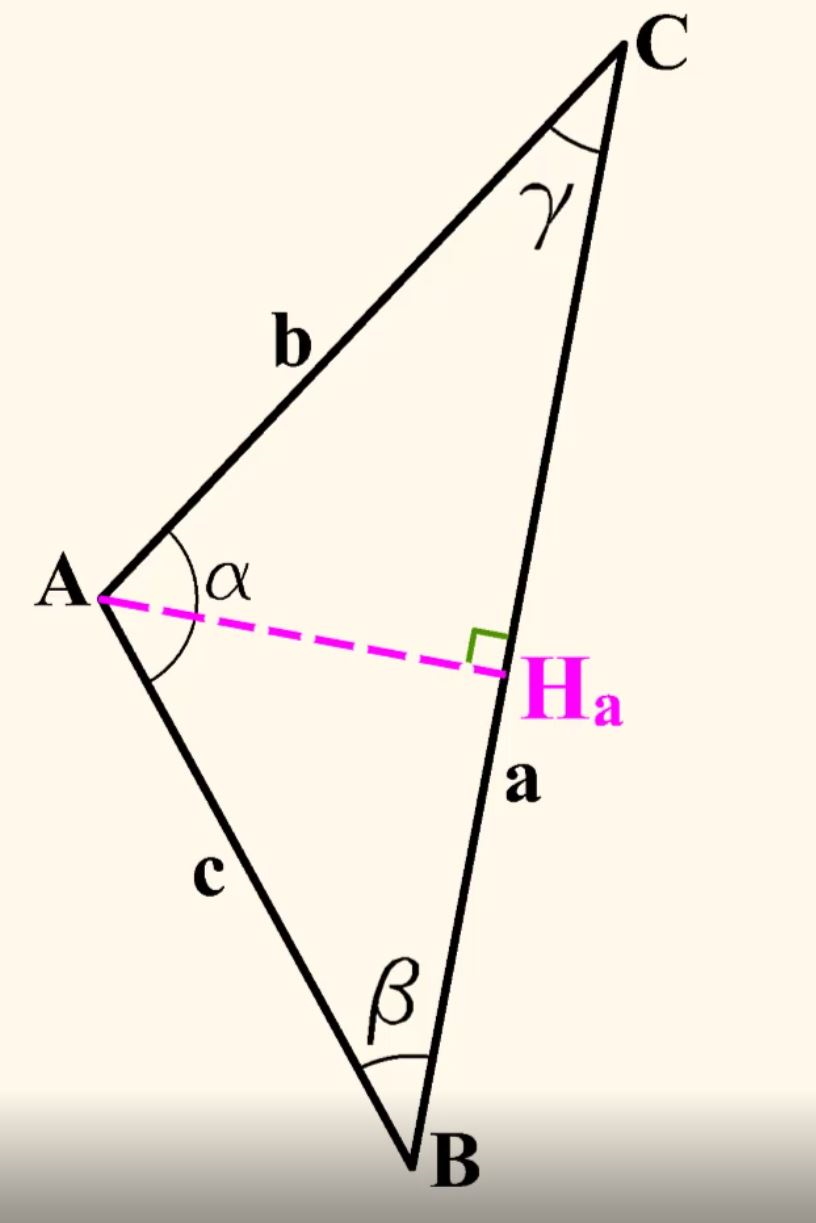
La dimostrazione parte da un triangolo generico ABC i cui lati, opposti ai corrispondenti vertici, misurano a, b e c. Gli angoli corrispondenti ai tre vertici sono alfa, beta e gamma. (Figura 2)
Si dimostra l’enunciato con riferimento al lato b.
E allora, per prima cosa tracciamo l’altezza AHa relativa al lato a del triangolo.
Applicando poi il teorema di Pitagora ai due triangoli rettangoli ABHa e AHaC ricaviamo il quadrato di AHa come differenza tra il quadrato dell’ipotenusa e il quadrato dell’altro cateto.

Eguagliando le due espressioni di AHa (Figura 3) e osservando che CHa è uguale ad a meno BHa e che BHa è uguale a c per coseno di beta, eseguiti gli opportuni passaggi di tipo numerico, arriviamo alla conclusione della dimostrazione:
Il quadrato del lato b del triangolo qualunque ABC è pari alla somma dei quadrati del lato a e del lato c meno il doppio prodotto di a per b per il coseno dell’angolo compreso tra a e b che vale beta.

La stessa dimostrazione viene poi eseguita a partire dall’altezza BHb relativa al lato b.
In questa seconda dimostrazione calcolo il lato c. (Figura 4)
La terza dimostrazione eseguita con riferimento all’altezza CHc relativa al lato c è lasciata come esercitazione per gli studenti.
L’esercizio numerico finale consiste in un triangolo ABC di cui conosciamo due lati rispettivamente di 238 metri e di 280 metri e l’angolo compreso tra questi due lati che ammonta a 108°. (Figura 5)
L’obiettivo è il calcolo del terzo lato del triangolo con l’applicazione del teorema coseno.
A conti fatti, il terzo lato varrà 419,80 metri.

Troverete l’applicazione del teorema del coseno nella lezione sulla somma di due vettori e nella lezione sulla differenza tra due vettori.
